ROC-Kurve
ROC-Kurve (receiver operating characteristics)
ACOMED statistik ist ein Statistik-Dienstleister mit dem Schwerpunkt der Planung und Auswertung von diagnostischen Studien. Darüber hinaus unterstützen wir Unternehmen der Pharmaindustrie, Medizinprodukte-Industrie
sowie CRO der der statistischen Planung und Auswertung klinischer Studien sowie bei der SAS-Programmierung. Wir bieten weiterhin Statistik-Beratung
und Statistik-Weiterbildungen
an.
Auf dieser Seite finden Sie einige Hinweise zu ROC-Kurven, Ihrer Berechnung, ihrem Anwendung und ihrer Interpretation. Wenn Sie Unterstützung bei der Planung und Analyse Ihrer diagnostischen Studie benötigen, zögern Sie nicht, Kontakt mit uns aufzunehmen (Tel.: +49 (0) 341 3910195).
ROC-Kurven (Receiver-Operating-Characteristics) geben einen Überblick über die diagnostische Güte eines diagnostischen Tests. In ihnen werden für verschiedene Cut-Off-Werte - in der Regel wird jeder Messpunkt verwendet - die Richtig-Positiv-Rate der Falsch-Positiv-Rate gegenübergestellt. Die Richtig-Positiv-Rate (TPF) entspricht der Sensitivität, die Falsch-Positiv-Rate (FPF) der Differenz 1-Spezifität (man beachte die umgekehrte Skalierung des x-Achse, wenn die Spezifität angegeben wird).
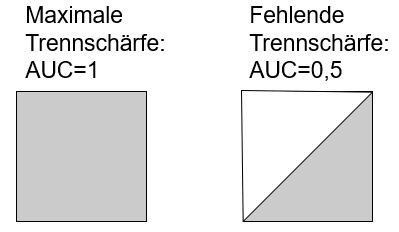
Ein Test weist keine diagnostische Güte auf, wenn TPF = RPF. Dies ist die Diagonale von links unten nach rechts oben (graue Linie in Abb.).
In der Abbildung wird die ROC-Kurve mit ihrem Konfidenzband gezeigt. Zudem sind ausgewählte Cut-Off-Werte angegeben.
ROC-Kurven sind u. a. ein Tool zur Auswahl von Cut-Off-Werten, nähere Informationen finden Sie hier.
Der diagnostische Test weist eine Trennschärfe auf, wenn sich die Kurve signifikant von der Diagonalen (links unten - rechts oben) unterscheidet. Im Idealfall (100%ige Trennschärfe) liegt die Kurve auf der linken bzw. oberen Begrenzungs-Seite des umschließenden Quadrates.
Ein Maß für die Güte des Tests ist die Fläche unter der ROC-Kurve (AUC: Area Under Curve). Die Fläche kann Werte zwischen 0,5 und 1 annehmen, wobei ein höherer Wert die bessere Güte anzeigt. AUC berechnet man am einfachsten mit der Trapezmethode, die im allgemeinen die Fläche gut abschätzt.
Die Fläche unter der Kurve AUC ist ein Übersichtsmaß und charakterisiert nicht
die diagnostische Güte im regulatorischen bzw. klinischem Sinn. Im klinischen Kontext wird ein Test für eine bestimmte Falsch-Negativ-Rate oder eine bestimmte Falsch-Positiv-Rate (bzw. Bereiche) eingesetzt, d. h. man überlegt sich, ob man eher Falsch-Positive oder eher Falsch-Negative in Kauf nimmt. Die korrekte Angabe der diagnostischen Güte ist also ein Wertepaar {Sens; Spec}, alternativ ist auch die Angabe der Vorhersagewerte {PPV; NPV} oder (selten) der Diagnostischen Likelihood-Ratios {DLR+, DLR-} möglich.
Dass die Angabe der Fläche nicht zielführend sein kann, macht folgende Abbildung deutlich:
Im nebenstehenden Beispiel, dass sich auf 3 Tumormarker beim Bronchialkarzinom bezieht (Daten aus Keller T et al. (1998): Tumour markers in the diagnosis of bronchial carcinoma: new options using fuzzy logic based tumour marker profiles. J Cancer Res Clin Oncol 124: 565-574) ist die AUC für Cyfra 21-1 deutlich (und statistisch signifikant) größer als die AUC für die beiden anderen Marker.
Im klinisch relevanten Bereich (hohe Spezifitäten) unterscheiden sich die Sensitivitäten von Cyfra 21-1 und CEA jedoch kaum. Die AUC ist also nicht hilfreich, um die diagnostische Güte im klinischen Einsatz sicher zu bewerten.
Weitere Hinweise zu ROC-Kurven
Die Fläche unter den ROC-Kurven folgen der selben Statistik wie nichtparametrische, vergleichende Rang-Tests (Wilcoxon-Statistik). Die Signifikanz einer AUC ggü. der Diagonalen ist also einfach mit den üblichen Tests (Mann-Whitneys U-Test) auszurechnen. Auch die AUC (vgl. ROC-Tool 1) lässt sich direkt aus dieser Statistik schätzen: AUC=U/(N1*N2), U- Testgröße der Wilcoxon-Statistik, N1 und N2 - Gruppenumfänge).
Deshalb sind ROC-Kurven nicht nur für quantitative Merkmale geeigent, sondern auch für qualitative Merkmale, die sich ordnen lassen (Ordinalskala), wie z. B. Befunde von Röntgenbildern, Scores etc.
Vergleich von ROC-Kurven (Test auf Unterschied von AUC, vgl. ROC-Tool 2) sind komplex. Entscheidend ist zunächst, ob die ROC-Kurven am selben Patientengut erhoben wurden oder nicht (verbundene vs. nicht verbundene Stichproben). Bei sich überschneidenden ROC-Kurven ist es sinnvoll, sie z. B. nur in einem ausgewählten Spezifitätsbereich zu vergleichen.
Ein Ausweg ist die Verwendung von Vierfelder-Tafeln für entweder gleiche Spezifitäten (dann: Vergleich der Sensitivitäten) oder Sensitivitäten. (dann: Vergleich der Spezifitäten). Diese Tafeln kann man dann mit Hilfe des McNemar-Tests (verbundene Stichprobe, mehrere Test werden in einer Studie untersucht; dies ist die Regel bei derartigen Auswertungen) oder des Chi2-Tests (unverbundene Stichprobe) vergleichen.
Der Anstieg der Gerade, die den linken unteren Nullpunkt mit einem Punkt auf der ROC-Kurve verbindet (blau), gibt das DLR+. Der Anstieg der Gerade, die den Punkt mit der rechten oberen Ecke verbindet (grün), das DLR-.
Sie können 2 Excel-Tools für ROC-Kurven erwerben.
(siehe Abbildungen unten: links: eine ROC-Kurve, rechts: Vergleich von 2 ROC-Kurven verbundener Daten,
lauffähig unter Excel 2000 und jüngere Versionen, Windows-Umgebung).
Kosten: 20 € je Tool. Bitte per E-Mail (info@acomed-statistik.de) anfragen.
ROC-Kurven können Sie auch mit den Software-Programmen Analyse-It, Medcalc, SPSS, SAS (dort als Teil der PROC LOGISTIC), GraphPad Prism u. a. erzeugen.
Excel-Tool ROC-Kurve (Anzeige ROC-Kurve, Berechnung der AUC inkl. Konfidenzintervall, Schätzung von Sensitivitäten für vorgegebene Spezifitäten, Schätzung von Spezifitäten für vorgegebene Sensitivitäten. Eingabe der Variablen im Longformat (1 Spalte für Messwerte, 1 Spalte für Krankheitsgruppe).
Excel-Tool 2 ROC-Kurve (Anzeige ROC-Kurven, Berechnung der AUC und deren Differenz, jeweils inkl. Konfidenzintervall, p-Wert für Vergleich. Eingabe der Variablen im Longformat (1 Spalte für Messwerte, 1 Spalte für Krankheitsgruppe).
